Завершение темы деревьев
Структуры данных для работы с числами
На этой лекции мы рассмотрим структуры данных, которые эффективно работают с числами в диапазоне до \( 2^w \), где w - это размер машинного слова (обычно 32 или 64 бита).
Основные операции
Мы хотим, чтобы наша структура поддерживала следующие операции:
add(x)- добавление элемента xremove(x)- удаление элемента xfind(x)- поиск элемента xnext(x)- нахождение минимального y, такого что y > xprev(x)- нахождение максимального y, такого что y < x
Эти операции позволят нам эффективно манипулировать данными и выполнять различные алгоритмические задачи.
Мы научимся делать операции за O(w), а потом за O(log w)
Битовый бор (trie)
Мы будем хранить числа хитрым образом, используя структуру данных, называемую битовым бором или префиксным деревом (trie).
Принцип работы битового бора:
-
Представление чисел: Каждое число представляется в двоичной форме (добиваем ведущими нулями до размера w)
-
Структура дерева:
- Корень дерева представляет пустую строку.
- Каждый узел (кроме корня) соответствует одному биту (0 или 1).
- Путь от корня до листа представляет число в двоичной форме.
-
Хранение чисел:
- Число хранится как путь от корня до листа.
- Каждый уровень дерева соответствует позиции бита в числе.
-
Преимущества:
- Эффективное использование памяти для чисел с общими префиксами.
- Быстрый поиск, вставка и удаление (O(w), где w - длина числа в битах).
-
Операции:
add(x): Добавляем путь для двоичного представления x.remove(x): Удаляем путь, соответствующий x.find(x): Проходим по пути, соответствующему x.next(x)иprev(x): Используем структуру дерева для эффективного поиска.
Пример:
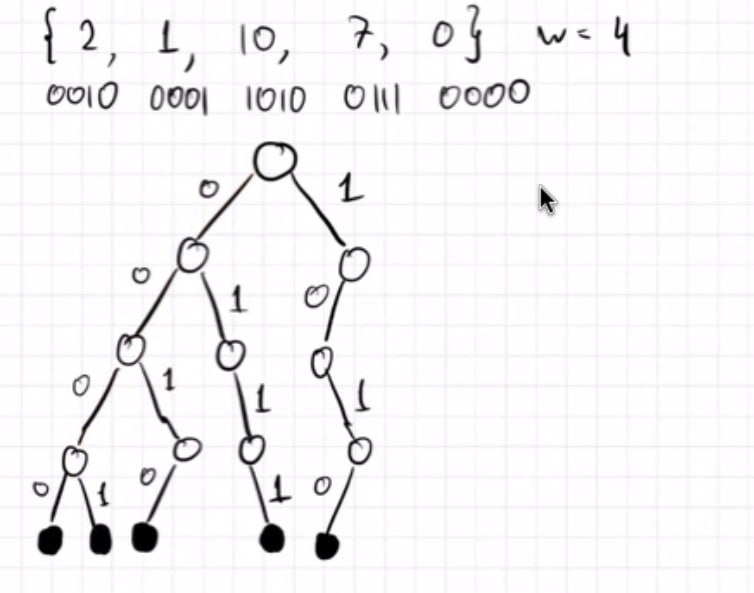
В данном случае мы считали, что числа не совпадают, но никто не мешает нам в листах хранить число --- количество чисел приходящих в этот лист.
Время O(w), Память O(nw).
Быстрый цифровой бор (x-fast trie)
X-fast trie - это усовершенствованная версия обычного битового бора, которая позволяет выполнять операции быстрее, за счет использования дополнительной памяти.
Как у нас работал next(x)?
-
Прочитать x (спуск) --- O(w)
-
Пойти направо (подъем + спуск в сына) --- O(w)
-
Идти до конца влево (спуск) --- O(w)
Мы можем это ускорить:
Основные идеи:
-
Хеширование префиксов:
- Для каждого уровня бора создаем хеш-таблицу.
- В хеш-таблице хранятся все префиксы, существующие на данном уровне.
-
Двоичный поиск по уровням:
- Вместо прохода сверху вниз, используем двоичный поиск по уровням бора. Благодаря хеш-таблицам из пункта 1. это происходит быстро.
-
Связи между уровнями:
- Каждый узел хранит указатели на свой наименьший и наибольший лист-потомок.
Благодаря этому мы умеем делать вторую и третью операцию у next за O(1), а первую за O(log w).
Операции:
Теперь наши операции делают еще:
-
find(x): O(log w)
- Используем двоичный поиск по уровням, чтобы найти наибольший существующий префикс x.
-
next(x) и prev(x): O(log w)
- Находим наибольший существующий префикс x.
- Используем указатели на листья для быстрого перехода к следующему/предыдущему элементу.
todo: описать функцию next_or_prev с лекции и в целом распиши поподробнее я не выкупил
- add(x) и remove(x): O(w)
- Обновляем все уровни и соответствующие хеш-таблицы.
Преимущества:
- Операции find, next и prev выполняются за O(log w) вместо O(w).
- Сохраняет преимущества обычного бора в представлении чисел.
Недостатки:
- Требует O(nw) памяти, что может быть значительно при больших n и w.
- Операции вставки и удаления остаются O(w).
Сверхбыстрый цифровой бор (y-fast trie)
Y-fast trie - это дальнейшее улучшение x-fast trie, которое позволяет достичь лучшей производительности и эффективности использования памяти.
Основные идеи:
-
Разделение на блоки:
- Разбиваем все числа на блоки размером O(log w).
- Каждый блок представлен одним представителем
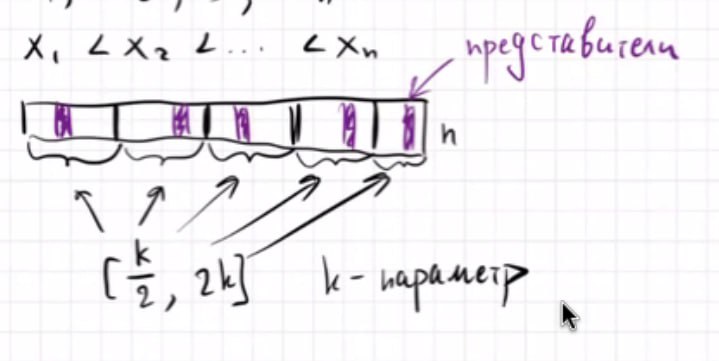
-
Использование сбалансированных деревьев:
- Внутри каждого блока используем сбалансированное двоичное дерево поиска (например, красно-черное дерево).
- Это позволяет эффективно управлять элементами внутри блока.
-
Двухуровневая структура:
- Верхний уровень: x-fast trie для репрезентативных элементов блоков.
- Нижний уровень: сбалансированные деревья для элементов внутри блоков.
Операции:
-
find(x): O(log w)
- Используем x-fast trie для нахождения нужного блока.
- Затем ищем элемент в сбалансированном дереве этого блока.
-
next(x) и prev(x): O(log w)
- Находим блок, содержащий x или следующий за ним.
- Используем сбалансированное дерево для точного поиска.
-
add(x) и remove(x): O(log w)
- Находим нужный блок.
- Обновляем сбалансированное дерево этого блока.
- При необходимости обновляем структуру блоков (разделение или слияние).
Преимущества:
- Все основные операции выполняются за O(log w).
- Значительно меньшее использование памяти по сравнению с x-fast trie: O(n) вместо O(nw).
- Сохраняет эффективность для операций поиска и обновления.
Недостатки:
- Более сложная реализация по сравнению с x-fast trie.
- Необходимость поддержания баланса между блоками.
Сравнение с другими структурами:
| Структура | Операции | Память |
|---|---|---|
| Битовый бор | O(w) | O(nw) |
| X-fast trie | O(log w) для find/next/prev, O(w) для add/remove | O(nw) |
| Y-fast trie | O(log w) для всех операций | O(n) |
Y-fast trie предоставляет оптимальный баланс между скоростью операций и использованием памяти, делая его эффективным выбором для многих приложений, работающих с большими наборами целых чисел.