Концепция
Известно, что с одним набором ключей можно построить большое количество различных деревьев поиска, так вот эту проблему можно устранить, добавив некоторой определенности к ключам, например дав каждому в пару приоритет и строя одновременно дерево поиска на ключах и кучу на приоритетах.
Отступление
На самом деле splay-дерево лучше чем декартово во всем, если мы будем сравнивать их как деревья поиска, так что если вы его знаете и декартач вам не нравится, или не заходит по времени, пишите splay.
Идея
Нам не важны приоритеты, которые мы даем ключам, поэтому давайте выдавать случайные приоритеты ключам. Дальше будет доказано, что в таком случае средняя глубина любой вершины будет \(O(\log n)\).
Реализация
В декартовом дереве все держится на 2 операциях: split и merge, реализуем их, а потом через них все остальное.
Merge(T1, T2)
Merge - объединение двух деревьев в одно, на деревья наложены ограничения, любой ключ из левого дерева меньше, чем любой ключ из правого. Наша реализация накладывает на нас ограничение: в итоге должна получиться куча на приоритетах, значит мы точно знаем, корнем будет вершина с наибольшим приоритетом, а вторая должна быть смерджена с одним из потомков будущего корня. Сложность работы - \(O(h)\).
Код
node *merge(node *l, node *r) {
if (l == nullptr) {
return r;
}
if (r == nullptr) {
return l;
}
if (l->y >= r->y) {
l->r = merge(l->r, r);
return l;
}
r->l = merge(l, r->l);
return r;
}
Split(T, x)
Split - разрез дерева на два по такому правилу: вершины с ключом, меньшим x окажутся в левом дереве, с большим - в правом(про равенство обычно не говорят, может быть там, где решит программист). Ну тут все совсем просто, начинаем алгоритм в корне, мы знаем, куда отойдет вершина, от которой мы запустились, а также знаем, куда отойдет поддерево одного из его сыновей, нужно просто запустить split от второго и привязать результат этого на место сына, от которого мы запустились. Сложность работы - \(O(h)\).
Код
pair<node *, node *> split(node *root, long long x) {
if (root == nullptr) {
return {nullptr, nullptr};
}
if (root->x <= x) {
auto res = split(root->r, x);
root->r = res.first;
return {root, res.second};
}
auto res = split(root->l, x);
root->l = res.second;
return {res.first, root};
}
Остальные операции
Кратко опишу логику остальных операций:
- insert (в начало/конец) - merge
- insert (в любое место) - split+split+merge+merge
- remove (первый/последний) - split
- remove (вырезание подотрезка ключей) - split+split+merge
Короче, удобно.
Математические свойства объекта
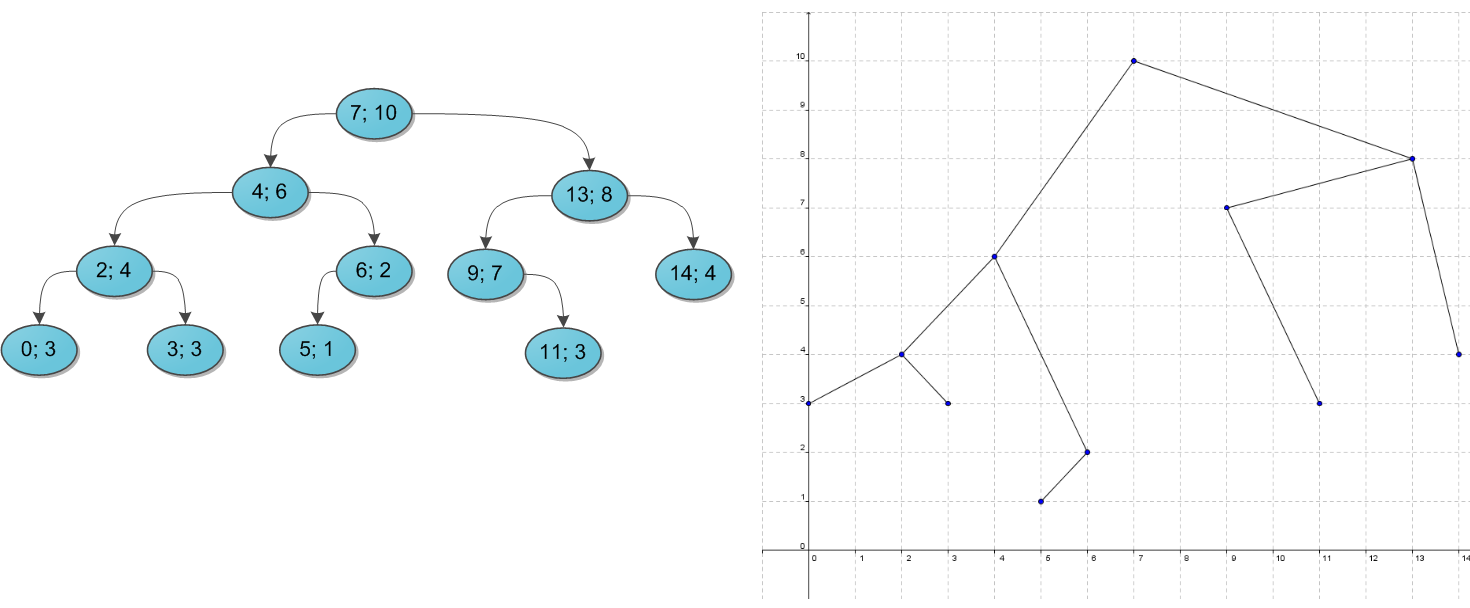
Единственность декартова дерева на заданном наборе пар ключ-значение
Начнем с более скучного факта: для заданного набора пар ключ-приоритет, в котором все ключи и приоритеты разные, декартово дерево строится единственным образом. Сам по себе факт бесполезный, но позволяет лучше понять структуру, с которой мы работаем.
Доказательство:
- Отсортируем все пары по значению ключа.
- Заметим, что корень у нас определяется единственным образом - вершина с наибольшим приоритетом.
- Все вершины левее этого корня будут в поддереве левого сына этой вершины, а вершины правее, наоборот, в поддереве правого сына. Разделим наш отрезок на 2 по этому принципу.
- Вернемся ко 2ому шагу этого алгоритма, но уже для этих подотрезков.
После того, как описанный выше алгоритм закончит работу, он построит декартово дерево на заданном ему наборе пар ключ-значение, так как у нас нигде не было выбора, то построенное дерево будет единственным.
Средняя глубина вершины
Давайте наконец докажем, что все операции в среднем работают за \(O(\log n)\), доказав, что именно такая средняя глубина вершины в декартовом дереве.
Доказательство:
Заметим, что глубина вершины \(v\) - кол-во вершин, которые являются предком вершины \(v\). Тогда докажем следующую лемму.
Лемма. В декартовом дереве вершина \(u\) - предок вершины \(v\), если на отрезке \([min(u, v), max(u, v)]\) в массиве пар, отсортированном по ключам - у вершины \(u\) максимальный приоритет.
Доказательство:
- Предположим у вершины \(u\) не максимальный приоритет, значит есть другая вершина на этом отрезке с большим приоритетом - \(t\).
- Вспомним прошлое доказательство единственности декартова дерева, в нем мы конструктивно его строили, если мы в том алгоритме остановимся на вершине \(t\), что будет раньше, чем для вершин \(u\) и \(v\), потому что приоритет у \(t\) меньше, то мы поймем, что \(u\) и \(v\) попадут в разные поддеревья, потому что находятся с разных сторон от \(t\), а значит \(u\) не может быть предком \(v\).
Докажем в обратную сторону:
- Пусть у нас \(u\) не предок вершины \(v\), но имеет наибольший приоритет на отрезке \([min(u, v), max(u, v)]\), тогда точно есть единственная вершина \(t\), для которой верно, что \(u\) и \(v\) ее потомки, и лежат в поддеревьях разных сыновей этой вершины.
- Что тогда мы знаем про \(t\):
- Она лежит между \(u\) и \(v\), потому что ее ключ между ключами \(u\) и \(v\).
- Ее приоритет больше, чем у \(u\) и \(v\).
- Получаем противоречие, есть вершина \(t\) на отрезке \([min(u, v), max(u, v)]\) с большим приоритетом, чем у \(u\).
Вернемся к основному доказательству, так как мы случайно брали приоритеты, то теперь мы знаем вероятность того, что вершина под номером \(u\) - предок вершины под номером \(v\) - \(\frac{1}{|u - v| + 1}\). Подсчитаем эту вероятность для вершины под номером \(k\): $$\sum\limits_{i=1}^{k-1}\frac{1}{k - i + 1}+\sum\limits_{j=k+1}^{n}\frac{1}{j - k + 1}\leq2*\sum\limits_{i=2}^n \frac{1}{i}=2\log{n}$$ Получили нужную нам асимптотику.
Неявное дд
Концепция
Мы хотим уметь делать то же самое, но на массиве значений, а то есть:
- Быстро объединять массивы
- Быстро вставлять в любое место массива подмассив
- Быстро делить массив на 2 подмассива
- Быстро делать массовые операции
- Быстро находить по ссылке на элемент его индекс в массиве
Под быстро тут везде подразумевается асимптотика \(O(\log n)\).
Идея
Заметим, что уже почти все готово, нужно просто как-то избавиться от дерева поиска по ключам, и мы получим нужную нам структуру данных. Также подметим, что из двух ключевых операций merge и split, на ключи опирается только split. Так давайте перепишем его так, чтобы теперь он переходил в сына не на основе ключа, который лежит в текущей вершине, а на основе размеров поддеревьев, и мы получим неявное дд. Неявным оно названо, потому что ключ теперь хранится неявно, и это на самом деле размер поддеревьев.
Измененный split
pair<node *, node *> split(node *root, long long k) {
if (!root) {
return {nullptr, nullptr};
}
if (size(root->l) >= k) {
auto res = split(root->l, k);
root->l = res.second;
upd_value(root);
return {res.first, root};
}
auto res = split(root->r, k - size(root->l) - 1);
root->r = res.first;
upd_value(root);
return {root, res.second};
}
В этом коде есть загадочные функции upd_value и size, про которые я еще не рассказал. Как я уже говорил выше, теперь мы ориентируемся на размеры поддеревьев, что означает, что нам нужно их где-то хранить, обычно под это заводится отдельное поле у вершины, которое и будет возращать size с проверкой на пустой указатель:
int size(node *x) {
if (!x) {
return 0;
}
return x->size;
}
Ну а upd_value занимается тем, что пересчитывает все внутренние переменные через детей при изменении структуры дерева. Это крайне удобно и я очень советую писать именно так, потому что далее будет рассказано про отложенные операции и функцию push, проталкивающую их и очень легко допустить ошибку и объединить эти функции в одну, как, например, происходит в до, и получить потом TL на каком-то хорошем тесте.
void upd_value(node *x) {
if (!x) {
return;
}
x->size = 1 + size(x->l) + size(x->r);
// Другие обновления через сыновей
}
Ленивое распространение
Идешь в душ, делай push! - Неизвестный мудрец, 201* год
Иногда хочется делать грязь с отрезками, например делать прибавление на них, присвоение, считать сумму, максимум, минимум, реверсить и так далее. Но ручками делать это долго. На помощь придет лень, а точнее ленивое распространение. Пусть у нас есть какая-то операция на отрезке, причем ВАЖНО: для каждой вершины мы знаем все изменения в ней, если эту операцию применить. Тогда давайте пользоваться таким классным свойством, предположим у нас есть вершина дд, отвечающая за отрезок, на котором эту операцию хочется применить. Заведем флажок, который будет обозначать, что нам нужно применить операцию к поддереву этой вершины, а когда посетим эту вершину, сделаем в ней изменения, чтобы получить корректные данные для нее, а флажок протолкнем в детей. Также важно, чтобы эти изменения не обязывали высчитывать промежуточные результаты в вершинах, например, мы можем присвоить значение \(x\) потомку не зная, какие изменения были в нем до, что позволяет нам проталкивать флаги нерекурсивно, а просто перезаписывая. Таким образом мы будем насчитывать реальные значения в вершинах мы будем только когда посещаем их и делаем push от них, а значит это не будет увеличивать сложность алгоритма.
Теперь чтобы в нашем неявном дд сделать прибавление на отрезке мы можем завести поле add, отвечающие за прибавление на отрезке у поддерева данной вершины, при запросе с помощью двух split'ов получать нужный отрезок, ручками менять поле у его корня и мерджить обратно. Очень удобно. Главное не забывать делать push всегда и везде. Вот его примерный код для сложения с подсчетом суммы на отрезке:
void push(node *x) {
if (x == nullptr) {
return;
}
if (x->add != 0) {
x->sum += x->size * x->add;
if (x->l) {
x->l->add += x->add;
}
if (x->r) {
x->r->add += x->add;
}
x->add = 0;
}
// Проталкивание других флагов
}
Персистентное дд
Как и дерево отрезков, дд можно сделать персистентным, для этого вам просто нужно при любом изменении в вершине создавать ее полную копию и делать изменение уже с ней. Просто модифицируйте split и merge так, чтобы они внутри и создавали копии вершин. Возникает одна проблема, при полном копировании теряется случайность приоритета, а если приоритет у клона задавать случайно, то он может поменять структуру дерева, если его приоритет случайно окажется больше, чем у предка. Если же приоритеты не менять, то пользователь может намеренно скопировать одну и ту же вершину много раз и мы получим бамбук и ухудшим асимптотику до линии. Решить эту проблему можно разными способами, но самым удобным мне показался вариант создания второго приоритета, который будет разным у клонов, сравнение приоритетов теперь надо делать по паре, причем сначала по первому значению, а затем по второму.