Дерево отрезков
Дерево отрезков (Segment Tree) — это структура данных, которая позволяет эффективно выполнять операции на отрезках массива. Основные операции, которые поддерживает дерево отрезков:
- Обновление элемента массива за O(log n)
- Вычисление функции (сумма, минимум, максимум и т.д.) на отрезке за O(log n)
Казалось бы, зачем нам ДО, когда мы можем более узкие функции, например, префиксные суммы . ДО - очень гибкая структура данных, которая поможет вам делать все эти операции вполне быстро.
RMQ - задача поиска минимума на отрезках
RSQ - задача поиска суммы на отрезках
Структура дерева отрезков
Дерево отрезков представляет собой бинарное дерево, где:
- Корень дерева соответствует всему массиву [0, n-1]
- Каждый узел соответствует некоторому отрезку [l, r]
- Листья дерева соответствуют отдельным элементам массива.
- Каждый внутренний узел имеет двух потомков: левый соответствует отрезку [l, mid], правый — отрезку [mid+1, r], где mid = (l + r) / 2
Построение дерева отрезков
Построение дерева отрезков выполняется рекурсивно:
// Массив для хранения дерева отрезков
int tree[4*MAXN];
// Функция построения дерева
void build(int a[], int v, int tl, int tr) {
if (tl == tr) {
tree[v] = a[tl];
} else {
int tm = (tl + tr) / 2;
build(a, v*2, tl, tm);
build(a, v*2+1, tm+1, tr);
tree[v] = tree[v*2] + tree[v*2+1]; // Для суммы на отрезке
}
}
Именно данная функция вам поможет, как она устроена. Наше дерево занимает O(n) памяти.
Пример ДО на суммы:
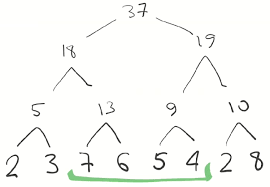
Запрос на отрезке
// Функция запроса суммы на отрезке [l, r]
int sum(int v, int tl, int tr, int l, int r) {
if (l > r)
return 0;
if (l == tl && r == tr) {
return tree[v];
}
int tm = (tl + tr) / 2;
return sum(v*2, tl, tm, l, min(r, tm))
+ sum(v*2+1, tm+1, tr, max(l, tm+1), r);
}
Мне эта реализация не нравится, потом перепишу.
Обновление элемента
// Функция обновления элемента
void update(int v, int tl, int tr, int pos, int new_val) {
if (tl == tr) {
tree[v] = new_val;
} else {
int tm = (tl + tr) / 2;
if (pos <= tm)
update(v*2, tl, tm, pos, new_val);
else
update(v*2+1, tm+1, tr, pos, new_val);
tree[v] = tree[v*2] + tree[v*2+1];
}
}
Фанфакты про дерева отрезков
-
Любой отрезок по l,r можно разбить на 2*log n вершин.
- Доказательство аналогично пункту 2.
-
Функция get делает не более 4*log n рекурсивных вызовов
-
Докажем по индукции по уровням отрезков. Корень очевидно. Давайте докажем, что на каждом слое мы делаем не больше 4 уровней.
-
База очевидна. В корне 1 вызов.
-
ИП: На текущем уровне есть 4 вершины и докажем, что из них вызовется не более 4 вершин. Посмотрим на границы(потому что вершины слева и справа от наших границ не запустятся и то, что между ними тоже не запустится). Я могу запуститься вниз максимум только от 2 из них. Откуда и правда побеждаем. (В данном случае мы "запускаем" максимум 4 снизу)
-
Итого вот такая вкусная структура данных.