LA (Level Ancestor)
Есть дерево. Есть запросы LA(v,k) - предок v на уровне k. Уровни индексируются снизу вверх
Первое очевидное решение это двоичные подъемы.
| Препроцессинг | Запрос |
|---|---|
| O(n log n) | O(log n) |
Long-Path Decompostion
Возьму неиспользованную верхнюю вершину. Возьму в ее поддереве самый глубокий лист, выделю путь от листа до выбранной вершины, помечу все вершины на пути неиспользованными и продолжу алгоритм
Пример:
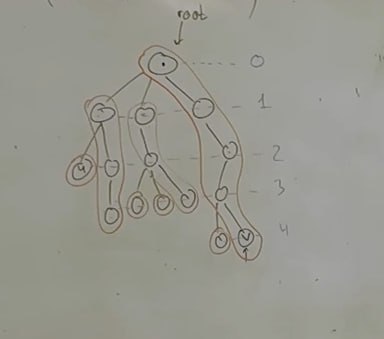
| Препроцессинг | Запрос |
|---|---|
| O(n) | O(sqrt n) |
Ladder Decompostion
Возьмем LPD, но увеличим высоту пути в 2 раза. Тадам
| Препроцессинг | Запрос |
|---|---|
| O(n) | O(log n) |
Ladder + Двоичные
Тут все очевидно
| Препроцессинг | Запрос |
|---|---|
| O(n log n) | O(1) |
Micro-Macro tree
Теоретически, можно добиться сложности O(n) на предподсчет и O(1) на запрос, если вы хотите узнать как, или хотите более подробное описание всех предыдущих алгоритмов, читайте здесь.
HLD
То же самое, что и Long -Path, только теперь по весу вершины (количеству вершин в поддереве).