Деревья.
Деревья храним 2-умя образами:
- Храним родителей.
- Храним детей.
LCA
LCA(u,v) - Lowest Common Ancestor - это узел w, который является предком и u, и v, и находится на максимальной глубине в дереве. Другими словами, w находится ближе всего к u и v среди всех общих предков.
Более простая задача.
Давайте решим сначала более простую задачу. Я хочу понимать является ли u предком v.
У этого есть очевидное тупое решение, но мы люди не тупые => пишем умное.
Для этого запустим dfs из корня и для каждой вершины будем хранить время входа в вершину и время выхода.
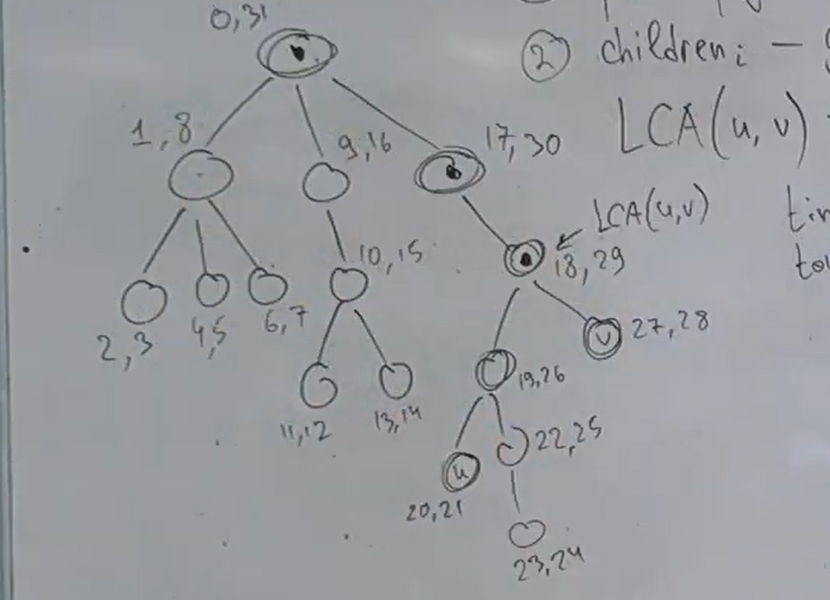
Ура, мы теперь умеем решать задачу LCA за линию. Будем поднимать одну вершину наверх, пока не выполнится описанное выше условие.
Двоичные подъемы.
Двоичное поднятие (подъемы) (Binary Lifting) (O(log n) времени на запрос):
Концептуально мы берем прошлую идею и накручиваем на нее бин. поиск по тому, на сколько мы должны подняться
- Предварительно вычисляется таблица
up[i][node], где up[i][node] — предок узла node на расстоянии 2i. Как такое считать?up[0][v] = pvup[k][v] = up[k-1][up[k-1][v]]
- Во время запроса LCA используются двоичные представления расстояний, чтобы быстро "поднимать" узлы.
- Общая идея та же, что и в подходе с уровнями, но с более быстрыми операциями подъема. Этот метод отлично подходит для множества запросов LCA.
// n - высота дерева
for k = log n...0:, n
pu = up[k][u]
if(!isParent(pu, v)):
u = pu
| Препроцессинг | Запрос |
|---|---|
| O(n log n) | O(log n) |
Эйлеров обход
Пронумеруем вершины. Запустим dfs. Каждый раз, когда мы заходим в вершину, выписываем ее номер. У каждой вершины посчитаю редом глубину.
Общая идея:
- Для узлов u и v, найти их индексы первого вхождения в последовательности Эйлерова обхода (first[u] и first[v]).
- Найти узел с минимальным уровнем в диапазоне
[first[u], first[v]](или[first[v], first[u]], если first[v] < first[u]) в массиве уровней. Этот узел является LCA(u, v).
Это следует из пары фактом про этот отрезкок.
- На отрезке есть LCA.
- У LCA min глубина.
- Нет других вершин с min глубиной.
Надо научиться считать минимум на отрезке. Например с помощью ДО.
Итого:
| Препроцессинг | Запрос |
|---|---|
| O(n) | O(log n) |
Sparse Table.
st[k][i] = min на [i, i + 2^i)
Оно будет считаться примерно так:
st[k][i] = min(st[k-1][i], st[k-1][i + 2^(k-1)])
Итого, искав так минус мы для LCA получаем вот такой результат:
| Препроцессинг | Запрос |
|---|---|
| O(n log n) | O(1) |
Алгоритм Фарах-Колтон и Бендор
Разобьем на блоки размера B. Ищем минимум на целых блоках. и на краешках.
Для каждого блока считаем префиксные и суффиксные минимумы.

Дальше идет грязь. Каждый блок у нас выглядит как массив из +-1, например так:

И теперь предподсчитаем все такие массивы из +-1. Это будет работать за 2^B B^3. Можно сделать O(n).
Все это один большой кеш мисс.