CT Notes y2024

Binary Search Tree

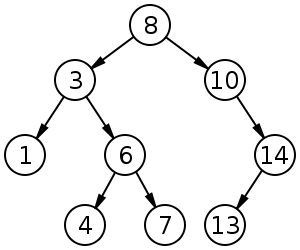
BST или бинарное дерево поиска.

Это абстрактный термин, существует множество разновидностей бинарных деревьев поиска, все они удовлетворяют нескольким аксиомам:

1. Являются бинарными деревьями, что следует из названия (тык, если вдруг не знаете, что это).
2. В каждой вершины дерева записано значение, называемое его ключом.
3. Если v - вершина бинарного дерева со значением x, то все узлы в левом поддереве должны иметь ключи, меньшие x, а в правом поддереве большие x.

Полезный факт. Если вам могут вставлять некоторые числа повторно, то вы можете у каждой вершины завести дополнительный параметр, равный числу данных элементов в структуре.

Список операций, доступных для дерева поиска:

1. add(x)
2. find(x)
3. remove(x)

Список операций у бинарных деревьев аналогичен списку операций у куч.

Утверждение. Все работает за O(h), где h - высота дерева.

Доказательство:

1. add(x)

   Алгоритм:

   1. Стартуем алгоритм с корня
   2. Если мы сейчас в вершине, сравниваем ключ, который в ней лежит и тот, что мы хотим добавить, в зависимости от этого идем в нужную сторону, чтобы выполнялось третье условие БДП.
   3. Если мы покинули дерево, то создаем новую вершину в том месте, где дерево было покинуто, она и будет вершиной с новым значением, заметим что ни одно из правил не нарушилось.

2. find(x)

   Алгоритм:

   1. Стартуем алгоритм с корня
   2. Если мы сейчас в вершине, сравниваем ключ, который в ней лежит и тот, что мы ищем, при равенстве мы победили и нашли искомый ключ, в противном случае идем в нужную сторону, пользуясь третьим условием БДП.
   3. Если мы покинули дерево, то искомого ключа в дереве нет.

3. remove(x)

   Алгоритм:

   1. Используем алгоритм поиска, который я описал выше и находим вершину, которую нужно удалить

   2. Тут есть несколько вариантов развития событий:

      1. Если вершина не имеет потомков, то просто удаляем ее
      2. Если у вершины один потомок, то мы просто вырезаем ее, а потомка привязываем к родителю вершины.
      3. Если у вершины есть оба потомка, то попытаемся свести этот случай к предыдущему, для этого найдем вершину с одним потомком, которого мы можем поменять местами с нашей, так, чтобы свойства БДП не нарушились. Оказывается такая вершина существует, мы можем спуститься в правое поддерево и в нем постоянно идти влево, что приведет нас к наименьшей вершине, большей исходной. Теперь просто меняем их местами и вырезаем желаемую вершину.

      

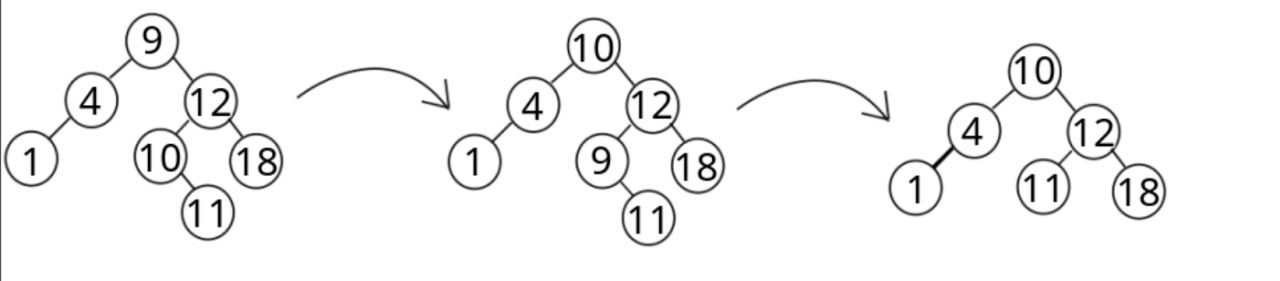
AVL-tree

AVL-дерево - бинарное дерево поиска, удовтлетворяющее свойству сбалансированности:

Для каждой вершины модуль разницы высот у поддеревьев ее сыновей не превышает 1(если сын отсутствует, считаем глубину его поддерева равной 0).

Мы поддерживаем h(x) --- количество вершин в поддереве, начинающегося с x.

h(v) = max(h(L),h(R)) + 1.

Лемма. В дереве высоты h хотя бы F_h вершин (h - ое число Фибоначчи)

Доказательство:

Пусть f(h) - min кол-во детей вершин в AVL c высотой h. Попытаемся вывести минимальное f(h), через предыдущие. У нас обязательно есть 1 корень, у него потомок глубиной хотя бы h-1, и второй, глубиной хотя бы h-2 из-за сбалансированности дерева. Получаем формулу, которая крайне похожа на формулу чисел Фибоначчи:

f(h) = f(h-1) + f(h-2) + 1

Числа Фибоначчи растут экспоненциально, что означает, что глубина нашего дерева будет логарифмической, если мы сможем поддерживать сбалансированность, научимся же это делать.

Балансировка AVL-tree

Предположим мы теоритически научились балансировать поддеревья для данной вершины не ломая сбалансированность потомков, как пользоваться такой суперсилой? Давайте при изменении структуры дерева, начнем из вершины, в которой это изменение произошло, будем подниматься до корня и балансировать вершину, которую проходим. Эта идея позволит вернуть сбалансированность дереву, потому что глубины остальных поддеревьев при добавлении/удалении не поменялись, а в тех вершинах, где что-то могло сломаться, мы все починили.

Ну а балансировать поддеревья сыновей фиксированной вершины нам поможет данный агрегат:

Всего существует 4 типа поворотов, я подскажу вам как их проще всего запомнить, если вы хотите сделать глубже поддерево правого сына, то вам нужно перекинуть туда вершины с левого поддерева, то есть повернуть штурвал вправо - поворот правый, иначе влево - поворот левый. Но это только первый критерий, есть еще второй - размер вращения. Если вам надо переместить всего 2 вершины и поддеревья, то это вращение малое, если же 3 вершины и поддеревья, то большое.

Я буду показывать только левые повороты, так как левые просто симметричны. Вот схема малого поворота:

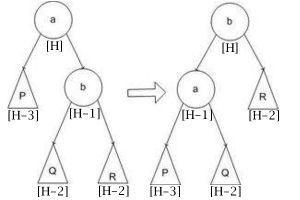
Он подойдет вам если глубина поддерева R равна h-2. При том, даже если глубина Q будет h-3, все равно балансированность дерева не нарушиться. Проверку этого замечательного факта и схемы я оставлю читателю, тут нечего особо обсуждать.

В том случае, если глубина R внезапно оказалась равна h-3, нам придется использовать большой левый поворот:

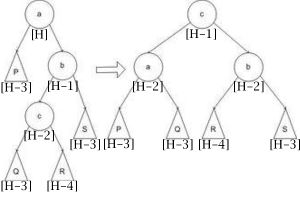
Тут на самом деле надо поразбирать вариантики, чему могут быть равный глубины поддеревьев Q и R, но проще заметить, что P и S всегда h-3, а мощности Q и R либо h-3, либо h-4, из чего уже становится понятно, что у полученных в результате поворота поддеревьев вершин a и b глубины действительно равны h-2. Ну а задание убедиться в том, что остальные свойства БДП выполняются при таком повороте я опять же оставлю читателю.

Последнее, что я хочу тут записать - как запомнить сами схемы поворота, попробуйте запомнить только перемещение вершин относительно друг друга, а перемещение поддеревьев восстановите автоматически.